El álgebra proposicional trata de determinar el valor de verdad de una combinación de enunciados se basa en reglas análoga, en primer lugar diremos que un enunciado -oración- es una proposición si es posible asignarle uno de los siguientes valores:
- verdadero (V)
- falso (F)
EJEMPLO:
las siguientes son proposiciones
- Hoy es lunes
- Llueve
- 2+3=4
- 2+3=5
no es necesario conocer si una afirmación es verdadera o falsa (es decir, su valor de verdad) para saber si es una proposición.
Nuestro sencillo estudio de las proposiciones no tratara de establecer el valor de verdad de una proposición dada, lo que haremos es analizar el valor de verdad de las proposiciones complejas, construidas con ciertas reglas a partir de proposiciones simples conociendo el valor de verdad de estas ultimas.
SÍMBOLOS DE LA LÓGICA PROPOSICIONAL:
Como ocurre en otras ciencias, es necesario en
lógica utilizar un lenguaje simbólico especial que
elimine los rasgos que no nos interesan y pongan de manifiesto
los que sí nos interesan. En lógica nos interesa
saber cómo están combinadas las
proposiciones , y no nos interesa en absoluto su significado. Por
ello necesitamos unos símbolos que, prescindiendo del
significado de las proposiciones, nos indiquen la forma
en que se combinan. Estos símbolos constituyen un
lenguaje formal.
CONECTIVOS LOGICOS
A continuación hay una tabla que despliega todas las conectivas
lógicas que ocupan a la lógica proposicional, incluyendo ejemplos de su
uso en el lenguaje natural y los símbolos que se utilizan para representarlas en lenguaje formal.

TABLAS DE VERDAD:
Tablas de verdad de las
conectivas lógicas
Existen conectores u operadores lógicas que permiten formar proposiciones compuestas (formadas por varias proposiciones). Los operadores o conectores básicos son:
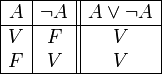
NEGACIÓN
NEGACIÓN
Palabras conectivas: no, no es cierto que, no es verdad que, nunca, carece de, sin, etc.
Prefijos negativos: a, des, in, i.
Condición: lo V se transforma en F (y al revés) P -p

CONJUNCIÓN:
Palabras conectivas: y, aunque, pero, mas, también, sin embargo, además, etc.
Condición: es V cuando ambas son V.
 Ejemplo:
Ejemplo:Sea el siguiente enunciado "el auto enciende cuando tiene gasolina en el tanque y tiene corriente en la batería"
Sean:
p= tiene gasolina el tanque
q = tiene corriente la batería
r = el auto enciende = p ^ q
La conclusión resultante es que para que el auto encienda se debe tener gasolina en el tanque y corriente en la batería, sino se tiene una de estas dos condiciones el auto no arrancará.
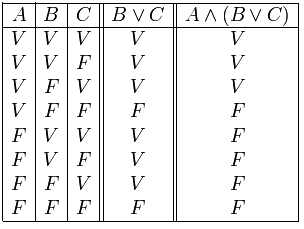
DISYUNCIÓN INCLUSIVA
Una, otra o ambas a la vez. (y/o)
Palabras conectivas: o
Condición: es F cuando las dos son F.
 Ejemplo:
Ejemplo:Sea el siguiente enunciado "Una persona puede entrar al cine si compra boleto u obtiene un pase"
Sean:
p= compra boleto
q = obtiene un pase
r = una persona entra al cine = p v q
La conclusión resultante es obvia, puesto que para entrar al cine es necesario tener por lo menos una de las dos condiciones: comprar un boleto o tener un pase, si se tiene ambas también se puede entrar, si no tengo ninguna de las dos alternativas entonces no se puede entrar al cine.
DISYUNCIÓN EXCLUSIVA
O una o la otra (NUNCA ambas juntas)
Palabras conectivas:
O ......... o .....
O bien .... o bien
.... a menos que ....
.... salvo que ......
Condición: es V cuando uno es V y el otro es F.

LA CONDICIONAL
Palabras conectivas: Si ..p.. entonces ..q.. Si ..p.. , ..q.. Cuando .......p............. , ......q.. Siempre ......p............. , ....q.. Es condición suficiente..p..para que..q.. .........q........ sólo si ......p....... Es condición necesaria...q..para que..p..
Condición: es falsa sólo si el antecedente (p) es V y el consecuente (q) es F. Ejemplo:
Ejemplo:
Si se tiene lo proposición "Si un cuerpo se calienta, entonces se dilata", se observa que estamos diciendo es que la primera proposición "si el cuerpo se calienta" implica a la segunda proposición " entonces se dilata", pero no se afirma que el antecedente es verdadero, ni el consecuente es verdadero, puede ser que el cuerpo no se calentó y el cuerpo se dilato por causa de otros factores ajenos a la temperatura, un golpe
 Ejemplo:
Ejemplo:Si se tiene lo proposición "Si un cuerpo se calienta, entonces se dilata", se observa que estamos diciendo es que la primera proposición "si el cuerpo se calienta" implica a la segunda proposición " entonces se dilata", pero no se afirma que el antecedente es verdadero, ni el consecuente es verdadero, puede ser que el cuerpo no se calentó y el cuerpo se dilato por causa de otros factores ajenos a la temperatura, un golpe
LA BICONDICIONAL
Palabras conectivas: si y sólo si; cuando y sólo cuando; es equivalente a; es condición suficiente y necesaria para; etc.
Condición: son verdaderas si ambas proposiciones tienen el mismo "valor de verdad".
Condición: son verdaderas si ambas proposiciones tienen el mismo "valor de verdad".
TAUTOLOGIAS, CONTRADICCION CONTIGENCIACon cinco conectivas lógicas básicas se construyen proposiciones compuestas que pueden ser tautologías, contradicciones o contingencias.
p ^ q --> p
TAUTOLOGÍA
EQUIVALENCIA LOGICA
(º, Û )
Dos
proposiciones P y Q en las mismas variables son equivalentes si y solamente si
tiene la misma tabla de verdad.
Se
denota P º Q ó P Û Q y se lee:
P
equivale lógicamente a Q, ó P y Q son equivalentes, P si y sólo si Q, P es
condición necesaria y suficiente para Q, Q es condición necesaria y suficiente
para P.
P º Q si y sólo si P « Q es una T
P º Q equivale a tener P Þ Q Ù Q Þ P
http://anderstivogm.blogspot.com/2010/05/conectivos-logicos-y-tabla-de-verdad.html http://www.academialap.com/Tablas_de_verdad_ejercicios_resueltos_I.html https://angelarendon.wordpress.com/2011/10/20/3-1-4-tautologias-contradiccion-y-contingencia-2/
cmap.upb.edu.co/rid=1153150359901...543/capitulo%20Logica.doc
|




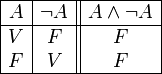
No hay comentarios.:
Publicar un comentario